MASA MASA SMA

Indah-Indahnya Masa SMA

09/16/2014

Kalau ditanya “hidup apa yang paling mudah?”, mungkin jawaban yang paling mendekati adalah hidup menjadi Nobita karena punya Doraemon, dan hidup di dunia Spongebob yang bahkan untuk bahagia cukup hanya dengan menempelkan rumput laut ke bibir.

Namun hidup ini bukanlah dunia Doraemon ataupun Bikini Bottom. Hidup ini nyata. Tapi tanpa kita sadari, atau mungkin sebenarnya udah sadar cuma nggak terlalu peduliin, bahwa ada satu tempat, lebih tepatnya satu fase kehidupan yang begitu surgawi. Begitu mudahnya kebahagiaan dirasakan pada fase itu.
Ya, fase itu adalah masa sekolah, khususnya, masa SMA.

Sumber: antah berantah

Buat anak-anak yang udah lulus, apalagi lulusnya udah lama banget, udah ngelewatin masa di mana ngelihat Facebook dan Path isinya postingan orang tentang pernikahan atau upload foto anaknya, masa SMA itu ngangenin banget. Kalau kita ingat-ingat lagi, masa SMA itu indah banget ya. Semuanya terasa lebih mudah.
Belajarnya
SMA beda banget sama kuliah. Waktu SMA, guru-guru yang ngejar-ngejar kita. Kalau kita nggak ikut ulangan atau ujian, ditanyain kenapa nggak ikut, terus dibujuk buat ikut susulan atau ujian pengganti. Di dunia kuliah, mahasiswa yang harus ngejar-ngejar dosen, karena mahasiswa yang butuh dosen. Dosen nggak mau ambil pusing. Kalau mahasiswa nggak datang, tinggal dikasih penilaian benar-benar sesuai kelakuan aja. Kalau SMA yang males masih di-naik-kelas-in, di kuliah, yang males ditinggalin.
Di kelas, guru yang nyamperin murid-muridnya dari kelas satu ke kelas lain. Muridnya cukup diem, nyiapin alat tulis. Bahkan udah segitu mudahnya pun, masih aja ada yang males. Kalau kuliah mahasiswa yang mesti pindah-pindah kelas ngikutin dosen itu ‘ngetem’-nya di ruangan yang mana.

Waktu SMA, di kelas bisa enak-enak banget mainan handphone pas guru lagi nerangin. Makanya, nggak heran banyak yang pake kerdus (kerudung dusta) ke sekolah cuma buat nyembunyiin earphone yang nyantol di kuping. Sebenernya pas kuliah juga bisa sih kayak gitu, tapi akibatnya mesti ditanggung sendiri. Pas SMA mah enak, nggak pernah merhatiin di kelas juga pas ujian sering dapet contekan. Lah kalau kuliah, ujian akhirnya sidang skripsi. Skripsinya bikin sendiri. Kalau nggak bener bikinnya, abis dibantai pas sidang.
Temennya
Indahnya masa SMA, nongkrongnya bisa sama yang begini. Cukup dengan modal menjadi anak cowok yang ‘lucu’ dan sedikit ‘involve’ di berbagai kegiatan si cewek, bisa jadi temen deketnya sampai punya akses sender-senderan pundak dan tentunya, foto bareng.

Instagram: hanikenisha

Udah kuliah mah boro-boro modusin cewek, yang ada ‘dimodusin’ mulu sama tugas. Nggak abis-abis.
Pas lulus-lulusan, bisa modus coret-coretan deket-deket dia, sampai modus nggak sengaja nyoret logo OSIS-nya.

Instagram: davianakbar

Waktu SMA juga, untuk nongkrong, khususnya buat yang anak cowok, rasanya nggak pernah sampe ngorogoh kocek sama sekali. Cukup dengan ngumpul di pinggir jalan setelah bel pulang sekolah, itu udah termasuk kategori nongkrong. Literally nongkrong. Jongkok di pinggir jalan, di depan warung. Beberapa ada yang ngerokok, beberapa lainnya ada yang cuma ikut-ikutan ngerokok. Kopinya nggak perlu yang seharga puluhan ribu sampe bikin puasa seminggu lalu harus difoto dan upload fotonya di Path dan Instagram, tapi cukup beli yang di warkop, segelas doang, diminum rame-rame.
Beda halnya dengan waktu SMA. Mungkin semester satu-dua masih bisa kayak gitu. Tapi semester berikutnya, nggak ada yang namanya murni nongkrong, tapi adanya nugas, nugas, dan nugas.

Janji pas mau lulus sekolah “Kalo udah lulus, kita harus tetap ngumpul ya…” seringnya hanyalah wacana belaka.

Makin akhir kuliahnya, atau pas udah lulus, makin susah lagi buat ngumpul. Nggak kelar-kelar. Pas semester susah ngumpul alasannya banyak tugas, semester akhir alasannya karena skripsi dan ada yang sambil kerja juga. Setelah lulus, janji-janji tetap ngumpul tinggallah wacana belaka. Udah lulus makin susah buat ngumpul, alasannya kerja terus, susah liburnya, kuliah bisa cabut tapi kerja nggak. Belum lagi kalau udah ada yang berkeluarga, makin susah. Ujung-ujungnya, sampe tua itu ngumpul nggak jadi-jadi.
Kekerenannya
Bagi anak SMA, keren itu sederhana. Buat yang cewek, cukup dengan pake sepatu putih kayak gini,

pake rok dan baju yang kekecilan, pake tas anak SD atau tas tante-tante sekalian (pokoknya nggak boleh tas anak sekolah), udah jadi gaul. Jangan lupa rambut belah tengah.
Buat cowok, cukup dengan baju dikeluarin, celana yang nggak boleh gombrong, dan tentu saja bagi sebagian besar kalangan, harus ngerokok. Kayak itu udah berasa keren.
Yang pasti, anak keren waktu SMA jalannya harus bergerombol dan berendeng kayak di Fear Factor gitu.

Intinya, waktu SMA, keren itu mudah, tinggal melanggar peraturan. Kata sekolah harus pake baju yang longgar, pakelah baju yang ketat. Kata sekolah rambut harus pendek, gondronginlah. Kata sekolah di kantin harus bayar, ngutanglah.
Pas kuliah juga bisa sih kayak gitu. Tapi bedanya, masa kuliah semua perbuatan ditanggung pelakunya sendiri. Di beberapa kampus ada yang ngewajibin pake pakaian/seragam tertentu. Kalau nggak nurutin, ya nggak boleh masuk, bahkan bisa sampai dikasih surat peringatan, bahkan bisa juga di-DO gara-gara itu. Yang membedakan jelas: pemakluman. Nggak ada lagi pemakluman saat sudah bukan lagi anak SMA.
Cintanya
Masa SMA itu adalah masa yang mudah.
Motor nggak sengaja sebelahan di parkiran aja udah ngerasa jodoh.
Nggak sengaja baris deketan pas upacara aja ngerasa udah jadi soulmate.
Absen atas-bawah udah ngerasa kamu sama dia nggak akan terpisahkan.
Ditunjuk guru untuk jadi teman sekelompok aja udah ngerasa memang ditakdirkan bersama.
Diminta PIN BBM atau nomer HP sama dia padahal buat nanyain tugas aja udah kayak diajak ngedate.
Di-chat buat nanyain tugas aja ngerasanya udah kayak ditanya “Will you marry me?”
Nggak sengaja beli somay di abang-abang yang sama di kantin aja langsung berasa akan hidup bersama selamanya.
Pake baju yang sama pas di sekolah aja langsung ngerasa “Dialah the one in my life.”
Ya, memang. Masa SMA adalah masa paling mudah. Atau lebih tepatnya, masa paling lemah.
Waktu SMA, untuk dapet pacar, simple banget. Cukup ikut ekskul yang keren, bawa motor dari duit bokap, punya jokes yang berhasil bikin dia ketawa. Kalau udah gitu, modal teh botol sama bercanda aja udah bisa jadian. Yang penting sekota, kalau bisa sesekolah, kalau bisa lagi, sekelas. Karena jarang banget anak SMA yang sanggup LDR.

Instagram: daraprayoga

Beda banget sama kehidupan selepas SMA. Untuk dapet pacar, masuk UKM yang ngetren aja belum cukup, tapi harus berprestasi banget juga. Punya kendaraan, kalau motor doang, apalagi cuma motor bebek atau matic, kadang nggak dilirik sama sekali, kalah sama yang bawa mobil (lagi-lagi, itu punya bokap). Untuk dapet pacar pada masa setelah SMA, harus punya kerjaan yang bagus, harus punya rencana masa depan, harus merhatiin keluarganya, asal-usulnya. Belum lagi berantem karena timpangnya kesibukan. Yang satu sibuk kerja, yang satunya lagi nganggur, sehingga salah satu menuntut waktu dan perhatian, namun yang satunya sedang nggak bisa diganggu. Belum lagi soal jarak. Belum lagi soal beda agama. Belum lagi soal restu.

MAULID NABI MUHAMAD

Peringatan Maulid Nabi pertama kali dilakukan oleh Raja Irbil (wilayah Irak sekarang), bernama Muzhaffaruddin Al-Kaukabri, pada awal abad ke 7 Hijriyah. Ibn Katsir dalam kitab Tarikh berkata:

Sultan Muzhaffar mengadakan peringatan Maulid Nabi pada bulan Rabi'ul Awal. Dia merayakannya secara besar-besaran. Dia adalah seorang yang berani, pahlawan, alim dan seorang yang adil – semoga Allah merahmatinya.

Dijelaskan oleh Sibth (cucu) Ibn Al-Jauzi bahwa dalam peringatan tersebut, Sultan Al-Muzhaffar mengundang seluruh rakyatnya dan seluruh ulama dari berbagai disiplin ilmu, baik ulama dalam bidang ilmu Fiqh, ulama Hadits, ulama dalam bidang ilmu kalam, ulama usul, para ahli tasawuf, dan lainnya. Sejak tiga hari, sebelum hari pelaksanaan Maulid Nabi, dia telah melakukan berbagai persiapan. Ribuan kambing dan unta disembelih untuk hidangan para hadirin yang akan hadir dalam perayaan Maulid Nabi tersebut. Segenap para ulama saat itu membenarkan dan menyetujui apa yang dilakukan oleh Sultan Al-Muzhaffar tersebut. Mereka semua berpandangan dan menganggap baik perayaan Maulid Nabi yang digelar untuk pertama kalinya itu.
Ibn Khallikan dalam kitab Wafayat Al-A`yan menceritakan bahwa Al-Imam Al-Hafizh Ibn Dihyah datang dari Maroko menuju Syam dan seterusnya ke Irak. Ketika melintasi daerah Irbil pada tahun 604 Hijriah, dia mendapati Sultan Al-Muzhaffar, raja Irbil tersebut sangat besar perhatiannya terhadap perayaan Maulid Nabi. Oleh karena itu, Al-Hafzih Ibn Dihyah kemudian menulis sebuah buku tentang Maulid Nabi yang diberi judul “Al-Tanwir Fi Maulid Al-Basyir An-Nadzir”. Karya ini kemudian dia hadiahkan kepada Sultan Al-Muzhaffar.
Para ulama, semenjak zaman Sultan Al-Muzhaffar dan zaman selepasnya hingga sampai sekarang ini menganggap bahwa perayaan Maulid Nabi adalah sesuatu yang baik. Para ulama terkemuka dan Huffazh Al-Hadits telah menyatakan demikian. Di antara mereka seperti Al-Hafizh Ibn Dihyah (abad 7 H), Al-Hafizh Al-Iraqi (w. 806 H), Al-Hafizh As-Suyuthi (w. 911 H), Al-Hafizh Al-Sakhawi (w. 902 H), SyeIkh Ibn Hajar Al-Haitami (w. 974 H), Al-Imam Al-Nawawi (w. 676 H), Al-Imam Al-Izz ibn Abd Al-Salam (w. 660 H), mantan mufti Mesir yaitu Syeikh Muhammad Bakhit Al-Muthi’i (w. 1354 H), mantan Mufti Beirut Lubnan yaitu Syeikh Mushthafa Naja (w. 1351 H), dan terdapat banyak lagi para ulama besar yang lainnya. Bahkan Al-Imam Al-Suyuthi menulis karya khusus tentang Maulid yang berjudul “Husn Al-Maqsid Fi Amal Al-Maulid”. Karena itu perayaan Maulid Nabi, yang biasa dirayakan pada bulan Rabiul Awal menjadi tradisi umat Islam di seluruh dunia, dari masa ke masa dan dalam setiap generasi ke generasi.
Para ahli sejarah, seperti Ibn Khallikan, Sibth Ibn Al-Jauzi, Ibn Kathir, Al-Hafizh Al-Sakhawi, Al-Hafizh Al-Suyuthi dan lainnya telah sepakat menyatakan bahwa orang yang pertama kali mengadakan peringatan maulid adalah Sultan Al-Muzhaffar. Namun juga terdapat pihak lain yang mengatakan bahwa Sultan Salahuddin Al-Ayyubi adalah orang yang pertama kali mengadakan Maulid Nabi. Sultan Salahuddin pada kala itu membuat perayaan Maulid dengan tujuan membangkitkan semangat umat islam yang telah padam untuk kembali berjihad dalam membela islam pada masa Perang Salib.
Ahmad bin ‘Abdul Halim Al Haroni rahimahullah mengatakan,
صَلَاحِ الدِّينِ الَّذِي فَتَحَ مِصْرَ ؛ فَأَزَالَ عَنْهَا دَعْوَةَ العبيديين مِنْ الْقَرَامِطَةِ الْبَاطِنِيَّةِ وَأَظْهَرَ فِيهَا شَرَائِعَ الْإِسْلَامِ
Artinya:
“Sholahuddin-lah yang menaklukkan Mesir. Dia menghapus dakwah ‘Ubaidiyyun yang menganut aliran Qoromithoh Bathiniyyah (aliran yang jelas sesatnya, pen). Shalahuddin-lah yang menghidupkan syari’at Islam di kala itu.”^[1]
Dalam perkataan lainnya, Ahmad bin ‘Abdul Halim Al Haroni rahimahullah mengatakan,
فَتَحَهَا مُلُوكُ السُّنَّة مِثْلُ صَلَاحِ الدِّينِ وَظَهَرَتْ فِيهَا كَلِمَةُ السُّنَّةِ الْمُخَالِفَةُ لِلرَّافِضَةِ ثُمَّ صَارَ الْعِلْمُ وَالسُّنَّةُ يَكْثُرُ بِهَا وَيَظْهَرُ
Artinya:
“Negeri Mesir kemudian ditaklukkan oleh raja yang berpegang teguh dengan Sunnah yaitu Shalahuddin. Dia yang menampakkan ajaran Nabi yang shahih di kala itu, berseberangan dengan ajaran Rafidhah (Syi’ah). Di masa dia, akhirnya ilmu dan ajaran Nabi shallallahu ‘alaihi wa sallam semakin terbesar luas.”^[2]
Sumber lain mengatakan perayaan Maulid yang sebenarnya diprakarsai oleh Dinasti Fatimiyyun sebagaimana dinyatakan oleh banyak ahli sejarah. Berikut perkataan ahli sejarah mengenai Maulid Nabi.
Al Maqriziy, seorang pakar sejarah mengatakan, “Para khalifah Fatimiyyun memiliki banyak perayaan sepanjang tahun. Ada perayaan tahun baru, hari ‘Asyura, maulid (hari kelahiran) Nabi, maulid Ali bin Abi Thalib, maulid Hasan dan Husain, maulid Fatimah az-Zahra, maulid khalifah yang sedang berkuasa, perayaan malam pertama bulan Rajab, perayaan malam pertengahan bulan Rajab, perayaan malam pertama bulan Sya’ban, perayaan malam pertengahan bulan Rajab, perayaan malam pertama bulan Ramadhan, perayaan malam penutup Ramadhan, perayaan ‘Idul Fithri, perayaan ‘Idul Adha, perayaan ‘Idul Ghadir, perayaan musim dingin dan musim panas, perayaan malam Al Kholij, hari Nauruz (Tahun Baru Persia), hari Al Ghottos, hari Milad (Natal), hari Al Khomisul ‘Adas (3 hari sebelum paskah), dan hari Rukubaat.”^[3]
Asy Syaikh Bakhit Al Muti’iy, mufti negeri Mesir dalam kitabnya mengatakan bahwa yang pertama kali mengadakan enam perayaan maulid yaitu: perayaan Maulid (hari kelahiran) Nabi shallallahu ‘alaihi wa sallam, maulid ‘Ali, maulid Fatimah, maulid Al Hasan, maulid Al Husain –radhiyallahu ‘anhum- dan maulid khalifah yang berkuasa saat itu yaitu Al Mu’izh Lidinillah (keturunan ‘Ubaidillah dari dinasti Fatimiyyun) pada tahun 362 H.^[4]
Begitu pula Asy Syaikh ‘Ali Mahfuzh dalam kitabnya Al Ibda’ fi Madhoril Ibtida’ (hal. 251) dan Al Ustadz ‘Ali Fikriy dalam Al Muhadhorot Al Fikriyah (hal. 84) juga mengatakan bahwa yang mengadakan perayaan Maulid pertama kali adalah ‘Ubaidiyyun (Fatimiyyun).^[5]

Perayaan di Indonesia

Festival Garebeg merayakan Maulid di Yogyakarta

Masyarakat Muslim di Indonesia umumnya menyambut Maulid Nabi dengan mengadakan perayaan-perayaan keagamaan seperti pembacaan shalawat nabi, pembacaan syair Barzanji dan pengajian. Menurut penanggalan Jawa, bulan Rabiul Awal disebut bulan Mulud, dan acara Muludan juga dirayakan dengan perayaan dan permainan gamelan Sekaten.

Perayaan di luar negeri

Perayaan Maulid di India.

Sebagian masyarakat Muslim Sunni dan Syiah di dunia merayakan Maulid Nabi. Muslim Sunni merayakannya pada tanggal 12 Rabiul Awal sedangkan muslim Syiah merayakannya pada tanggal 17 Rabiul Awal, yang juga bertepatan dengan ulang tahun Imam Syiah yang keenam, yaitu Imam Ja'far ash-Shadiq.
Maulid dirayakan di banyak negara dengan penduduk mayoritas Muslim di dunia, serta di negara-negara lain di mana masyarakat Muslim banyak membentuk komunitas, contohnya antara lain di India, Britania Raya, Rusia^[6] dan Kanada.^{[7] [8] [9] [10] [11][12] [13] [14][15]} Arab Saudi adalah satu-satunya negara dengan penduduk mayoritas Muslim yang tidak menjadikan Maulid sebagai hari libur resmi.^[16] Partisipasi dalam ritual perayaan hari besar Islam ini umumnya dipandang sebagai ekspresi dari rasa keimanan dan kebangkitan keberagamaan bagi para penganutnya.^[17]

LIRIK LAGU INDIA

Lirik lagu Raabta (Kehte Hain Khuda Ne) dari film Agent Vinod (2012)

Detail lagu:-
Judul lagu: Rabta (Night in Motel)
Film/Album: Agent Vinod
Penyanyi: Arijit Singh, Shreya Ghoshal, Hamsika
Music Director: Pritam
Pencipta lagu: Amitabh Bhattacharya
Panjang: 4:50
Music Label: T-Series

Lirik Raabta (Kehte Hain Khuda Ne)

Kehte hain khuda ne iss jahan mein sabhi ke liye
Kisi na kisi ko hai banaya har kisi ke liye
Tera milna hai uss rab ka ishaara maanu
Mujhko banaya tere jaise hi kisi ke liye
Kehte hain khuda ne iss jahan mein sabhi ke liye
Kisi na kisi ko hai banaya har kisi ke liye
Tera milna hai uss rab ka ishaara maanu
Mujhko banaya tere jaise hi kisi ke liye
Kuch toh hai tujhse raabta
Kuch toh hai tujhse raabta
Kaise hum jaane hume kya pata
Kuch toh hai tujhse raabta
Tu humsafar hai, phir kya fikar hai
Jeene ki wajah hi yahi marna issi ke liye
Kehte hain khuda ne iss jahan mein sabhi ke liye
Kisi na kisi ko hai banaya har kisi ke liye

Sa ni pa di na sa..

Meharbaani jaate jaate mujh pe kar gaya
Guzarta sa lamha ek daaman bhar gaya
Tere nazara mila, roshan sitaara mila
Takdeer ki kashtiyon ko, kinara mila

Sadiyon se tarse hai jaisi zindagi ke liye
Teri sauhbat mein duaayein hain ussi ke liye
Tere milna hai uss rab ka ishaara
Maanu mujhko banaya tere hi jaise kisi ke liye
Kehte hain khuda ne iss jahan mein sabhi ke liye
Kisi na kisi ko hai banaya har kisi ke liye
Tere milna hai uss rab ka ishaara
Maanu mujhko banaya tere hi jaise kisi ke liye
Kuch toh hai tujhse raabta
Kuch toh hai tujhse raabta
Kaise hum jaane hume kya pata
Kuch toh hai tujhse raabta
Tu humsafar hai, phir kya fikar hai
Jeene ki wajah hi yahi hai marna issi ke liye
Kehte hain khuda ne iss jahan mein sabhi ke liye
Kisi na kisi ko hai banaya har kisi ke liye

My Heart Goes All Dhin Tana - OST. NAVYA

 C#m              B

  

Kya batao dil khud hi na jaane
Apa yang aku  katakan hatiku tidak tahu
             A                      C#m
Kaise mehka mehka ehsaas hai
Bagaimana jenis perasaan ini
  C#m                          B
Ate jaate in lamhon ki lehron main
Aku memiliki moment seperti gelombang datang dan pergi
           A                         C#m
Kahin na kahin to kuch khaas hai
Maka di suatu tempat ada sesuatu yang istimewa

*)

C#m                 B
Na jaana kaisi hai yeh
Bagaimana cara untuk menuju kesana
         A                  E
Madhooshi hai kasia nasha
Ketidak sadaran ini seperti memabukan
C#m                 B
Hawa se kare batein
Hati ini berbicara sendiri
       A                    E
Yeh dil kyu kya hai wajah
Kenapa dengan hati ini apa alasanya

F#m                  E                   B   
Jahan yeh sara apna sa lage sapna sa lage
Seluruh dunia serasa milikku, seolah bermimpi

Reff

G#m         C#m                      A
Haan...na jane chala hai kya pane
Entah apa yang diinginkan,
 C#m  
Laga hai kyu gane
Kenapa ia bernyanyi
 A
My heart goes all dhin tana
Hatiku sangat gembira
 A
My heart goes oh all dhin tana
Hatiku sangat gembira

 C#m                   A
Thori thori betabian bhi
Bahkan sedikit ada kecemasan
  B                       G#m
Thora thora dil ko sukun hai
Hati ini sedikit merasa nyaman
 C#m                     A
Thori thori bechenian bhi
Bahkan sedikit ada kegelisahan
   B                        G#m
Thora thora chaya junun hai

Hati ini sedikit ada obsesi

Back to *)

My heart goes all dhin tana
Hatiku sangat gembira

 judul lagu: kuch na kahe

–FEMALE–
Kuch na kahe bas chup rahe
Jangan mengucapkan sepatah kata,cukup  kita diam saja
Khamoshiyaan hee keh jaaye
Biarkan kesunyian ini berbicara
Tham jaaye yeh jahan
Biarkan dunia ini datang
Aur pal bhi thaher jaaye
Dan bahkan waktu berhenti
–MALE–
Rahe na kuch bhi darmiyan
Biarlah tidak ada apa apa  di antara kita
Meete yeh saari dooriyaan
Semoga semua jarak ini segera lenyap
Milke bhi hai adhuri si
Bahkan setelah kita bertemu tampaknya tidak lengkap
Yeh daastan
Cerita ini
Rahe na kuch bhi darmiyan
Biarlah tidak ada apa apa  di antara kita
Meete yeh saari dooriyaan
Semoga semua jarak ini segera lenyap
Milke bhi hai adhuri si
Bahkan setelah kita bertemu tampaknya tidak lengkap
Yeh daastan
Cerita ini
–FEMALE–
Zidd yeh thi tumhe
Kau memiliki sikap keras kepala
Ke hum bhi kuch kahe
Kita juga harus mengatakan sesuatu
Hume yeh geela tha
Aku mengeluh padamu karena
Ke tum chup rahe
Kau tetap diam
–MALE–
Yeh majburiyaan aur yeh fasale
Dorongan ini dan jarak ini
Chaaha phir bhi badhte gaye
Bahkan keinginan ini masih tumbuh
–BOTH–
Ab jo yeh ehsaas hai
Sekarang semua perasaan ini
Yeh jo adhuri aas hai
Dan semua harapan ini tidak lengkap
Rehne de yuhi inhe jo zazbat hai
Biarkan mereka memiliki perasaan yang sama
Rahe na kuch bhi darmiyan
Biarlah tidak ada apa apa  di antara kita
Meete yeh saari dooriyaan
Semoga semua jarak ini segera lenyap
Milke bhi hai adhuri si
Bahkan setelah kita bertemu tampaknya tidak lengkap
Yeh daastan
Cerita ini
–CHORUS–
Rehke bhi sang hai juda
Bahkan setelah kebersamaan, kita tampaknya terpisah
Bhulega na kabhi jahan
Dunia ini tidak akan pernah lupa
Hai yeh alag hi daastan
Ini adalah cerita yang sama sekali berbeda
Saraswatichandra ki
Dari ‘Saraswatichandra’
Rehke bhi sang hai juda
Bahkan setelah kebersamaan, kita tampaknya terpisah
Bhulega na kabhi jahan
Dunia ini tidak akan pernah lupa
Hai yeh alag hi daastan
Ini adalah cerita yang sama sekali berbeda
Saraswatichandra ki
Dari ‘Saraswatichandra’

CARA SINGKAT MENGERJAKAN MATEMATIKA TINGKAT SMA

eh: Al Jupri

Dulu, ketika saya masih baru menjadi mahasiswa baru tingkat pertama, saya berkenalan dengan salah seorang mahasiswa baru lainnya yang di kemudian hari menjadi teman baik saya. Ketika awal perkenalan, kami pun ngobrol kesana-kemari. Tanya sana-tanya sini. Jawab sana, jawab sini. Hingga ia pun akhirnya bercerita bahwaa nilai tes Matematika Dasar-nya, yaitu salah satu mata pelajaran yang diujikan di UMPTN*, adalah 100 alias benar semua.

Mendengar ceritanya tersebut, saya pun terkagum-kagum dibuatnya. Dalam pikiran saya, saya berkesimpulan “Wah ia pasti orang yang sangat pandai”. Rasa kagum saya mendorong rasa ingin tahu saya tentang pengetahuannya dalam matematika. Akhirnya, dalam masa awal perkenalan itu, saya ajak ia ngobrol tentang matematika yang sudah pernah kami pelajari ketika semasa SD sampai SMA dulu.

Dari obrolan tersebut, saya jadi tahu, ternyata ia benar-benar luas pengetahuan tentang matematika yang sudah dipelajarinya. Hingga akhirnya, mungkin untuk menunjukkan kepiawaiannya, ia mengajak saya adu cepat mengerjakan soal matematika.

Mendapat tantangan itu, sebenernya saya ngeper juga. Karena saya merasa tak sepandai dirinya. Namun, karena ini namanya juga bukan lomba dan bukan apa-apa, saya sih mau saja waktu itu. Soal-soal pun dipilih secara acak dari buku kumpulan soal-soal latihan tes UMPTN* dan EBTANAS** beberapa tahun sebelumnya yang masih rajin ia bawa ke mana-mana. Kemudian, adu cepat menyelesaikan soal matematika pun dimulai.

Bagaimana hasilnya? Siapa yang tercepat?

Ternyata benar, dalam beberapa menit saja, teman saya itu berhasil menyelesaikan semua soal yang sudah dipilih tadi (karena yang dipilih cuma 3 soal sih). Dan ia keluar sebagai yang tercepat, menjadi pemenang. Sedangkan saya, satu soal pun belum mampu saya selesaikan. Waktu itu, saya terlalu berkutat dengan soal nomor pertama yang lumayan sukar untuk ukuran saya waktu itu. Walau sudah dengan segenap kemampuan saya berusaha menyelesaikannya, tapi ternyata, sampai waktu habis belum ketemu juga. Saya pun mengakui kelebihan dan kehebatannya.

Dengan sedikit malu-malu, saya bertanya padanya tentang soal yang belum bisa saya selesaikan tersebut. Sambil saya tanyakan pula kenapa ia begitu cepat bisa menyelesaikan soal-soal tersebut. Soal yang waktu itu belum bisa saya selesaikan adalah seperti berikut ini.

Soal: Bila a + 1/a = 5, maka nilai dari a³ + 1/a³ =…

Dengan cepat teman saya itu pun menyelesaikan soal tersebut seperti berikut ini:

a³ + 1/a³ = (a + 1/a)³ – 3a.1/a(a + 1/a) = 5³ – 3(5) = 125 – 15 = 110.

Melihat cara penyelesaiannya, saya hanya bisa melongo waktu itu. “Cuma satu baris? Padahal saya mencoba menyelesaikannya berbaris-baris, dan belum ketemu juga”, itu yang ada di pikiran saya. Kemudian, saya pun bertanya ke teman saya itu, kenapa cara pengerjaannya seperti itu?

Dengan senang hati, ia pun menjelaskan ke saya. Ia katakan bahwa, soal semacam tersebut dapat dengan mudah diselesaikan dengan rumus “cepat” berikut ini.

a³ + b³ = (a + b)³ – 3ab(a + b) ………………………………..(1)

Dengan mengganti b dengan 1/a, katanya, maka soal tadi dapat diselesaikan dengan cepat seperti yang sudah dikerjakannya tadi.

Saya yang tak terbiasa menggunakan rumus “cepat” ketika di SMA dulu, penasaran ingin tahu alasan kenapa rumus “cepat” tersebut bisa dipakai. Tapi sayang, teman saya itu tak memberi tahu saya. Malahan ia menambah lagi rumus cepat yang sudah ia ketahuinya, yaitu:

a³ – b³ = (a – b)³ + 3ab(a – b)……………………………….(2)

Akhirnya, ngobrol-ngobrol pun beres. Ia bergegas pulang menuju kost-kost-annya. Saya pun begitu, pulang dengan rasa penasaran yang mengganjal.

Di kost-kost-an, dengan penuh rasa penasaran ingin tahu, saya pun mengutak-atik rumus “cepat” yang telah ia gunakan tersebut. Setelah beberapa waktu lamanya, akhirnya, terpecahkan juga rahasia rumus “cepat” yang dipakai teman saya tersebut. Saya berhasil menelusuri asal-muasal rumus “cepat” tersebut, berhasil menguak rahasianya. (Duh rasanya begitu senang sekali, tak bisa saya ekspresikan dengan kata-kata).

Hasil penelusuran saya tersebut, setelah saya rapikan, seperti berikut ini.

(a + b)³ = (a + b)²(a + b)

= (a² + 2ab + b²)( a + b)

= a³ + a²b + 2a²b + 2ab² + b²a + b³

= a³ + b³ + 3a²b + 3ab²

= a³ + b³ + 3ab (a + b)

Jadi, (a + b)³ = a³ + b³ + 3ab (a + b).

Sehingga, a³ + b³ = (a + b)³ – 3ab (a + b). Rumus “cepat” (1) dapat saya buktikan kebenarannya. Kemudian, dengan cara serupa, saya pun berhasil menelusuri asal-muasal rumus “cepat” (2).

Walaupun apa yang telah saya lakukan tersebut sederhana, tapi bagi ukuran saya waktu itu adalah sesuatu yang menggembirakan hati, menyenangkan pikiran, dan memuaskan dahaga keingin-tahuan saya.

Sejak saat itu, bila ada rumus-rumus “cepat” yang saya temui di buku-buku bimbingan tes, saya pun terpacu untuk menelusuri asal-muasalnya. Dengan cara seperti itu, saya seringkali berhasil memecahkan rahasia rumus-rumus “cepat” yang selama ini beredar luas di kalangan siswa yang mengikuti bimbingan test.

Baiklah, segitu dulu saja ceritanya ya…, lain kali insya Allah saya akan membahas baik-buruknya penggunaan rumus “cepat” (Ada satu cerita yang sangat menggelikan tentang hal ini. Mau tahu? Silakan tunggu di postingan mendatang…). Sampai di sini dulu ya…, mudah-mudahan bermanfaat.

Sebagai bahan latihan untuk Anda, cobalah telusuri asal-muasal rumus-rumus “cepat” berikut ini.

1. Persamaan garis yang melalui titik (0, a) dan (b, 0) adalah ax + by = ab.
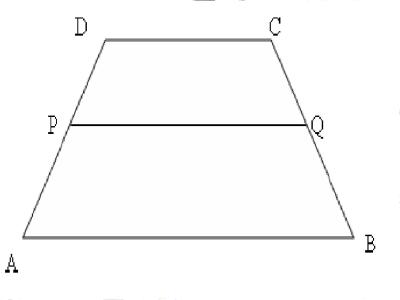
2. Perhatikan gambar berikut. Panjang PQ dapat ditentukan dengan mudah, yaitu:
   PQ = (AP. DC + DP. AB)/(AD)

Matematika

Dulu, ketika saya masih baru menjadi mahasiswa baru tingkat pertama, saya berkenalan dengan salah seorang mahasiswa baru lainnya yang di kemudian hari menjadi teman baik saya. Ketika awal perkenalan, kami pun ngobrol kesana-kemari. Tanya sana-tanya sini. Jawab sana, jawab sini. Hingga ia pun akhirnya bercerita bahwaa nilai tes Matematika Dasar-nya, yaitu salah satu mata pelajaran yang diujikan di UMPTN*, adalah 100 alias benar semua.

Mendengar ceritanya tersebut, saya pun terkagum-kagum dibuatnya. Dalam pikiran saya, saya berkesimpulan “Wah ia pasti orang yang sangat pandai”. Rasa kagum saya mendorong rasa ingin tahu saya tentang pengetahuannya dalam matematika. Akhirnya, dalam masa awal perkenalan itu, saya ajak ia ngobroltentang matematika yang sudah pernah kami pelajari ketika semasa SD sampai SMA dulu.

Dari obrolan tersebut, saya jadi tahu, ternyata ia benar-benar luas pengetahuan tentang matematika yang sudah dipelajarinya. Hingga akhirnya, mungkin untuk menunjukkan kepiawaiannya, ia mengajak saya adu cepat mengerjakan soal matematika.

Mendapat tantangan itu, sebenernya saya ngeper juga. Karena saya merasa tak sepandai dirinya. Namun, karena ini namanya juga bukan lomba dan bukan apa-apa, saya sih mau saja waktu itu. Soal-soal pun dipilih secara acak dari buku kumpulan soal-soal latihan tes UMPTN* dan EBTANAS** beberapa tahun sebelumnya yang masih rajin ia bawa ke mana-mana. Kemudian, adu cepat menyelesaikan soal matematika pun dimulai.

Bagaimana hasilnya? Siapa yang tercepat?

Ternyata benar, dalam beberapa menit saja, teman saya itu berhasil menyelesaikan semua soal yang sudah dipilih tadi (karena yang dipilih cuma 3 soal sih). Dan ia keluar sebagai yang tercepat, menjadi pemenang. Sedangkan saya, satu soal pun belum mampu saya selesaikan. Waktu itu, saya terlalu berkutat dengan soal nomor pertama yang lumayan sukar untuk ukuran saya waktu itu. Walau sudah dengan segenap kemampuan saya berusaha menyelesaikannya, tapi ternyata, sampai waktu habis belum ketemu juga. Saya pun mengakui kelebihan dan kehebatannya.

Dengan sedikit malu-malu, saya bertanya padanya tentang soal yang belum bisa saya selesaikan tersebut. Sambil saya tanyakan pula kenapa ia begitu cepat bisa menyelesaikan soal-soal tersebut. Soal yang waktu itu belum bisa saya selesaikan adalah seperti berikut ini.

Soal: Bila a + 1/a = 5, maka nilai dari a³ + 1/a³ =…

Dengan cepat teman saya itu pun menyelesaikan soal tersebut seperti berikut ini:

a³ + 1/a³ = (a + 1/a)³ – 3a.1/a(a + 1/a) = 5³ – 3(5) = 125 – 15 = 110.

Melihat cara penyelesaiannya, saya hanya bisa melongo waktu itu. “Cuma satu baris? Padahal saya mencoba menyelesaikannya berbaris-baris, dan belum ketemu juga”, itu yang ada di pikiran saya. Kemudian, saya pun bertanya ke teman saya itu, kenapa cara pengerjaannya seperti itu?

Dengan senang hati, ia pun menjelaskan ke saya. Ia katakan bahwa, soal semacam tersebut dapat dengan mudah diselesaikan dengan rumus “cepat” berikut ini.

a³ + b³ = (a + b)³ – 3ab(a + b) ………………………………..(1)

Dengan mengganti b dengan 1/a, katanya, maka soal tadi dapat diselesaikan dengan cepat seperti yang sudah dikerjakannya tadi.

Saya yang tak terbiasa menggunakan rumus “cepat” ketika di SMA dulu, penasaran ingin tahu alasan kenapa rumus “cepat” tersebut bisa dipakai. Tapi sayang, teman saya itu tak memberi tahu saya. Malahan ia menambah lagi rumus cepat yang sudah ia ketahuinya, yaitu:

a³ – b³ = (a – b)³ + 3ab(a – b)……………………………….(2)

Akhirnya, ngobrol-ngobrol pun beres. Ia bergegas pulang menuju kost-kost-annya. Saya pun begitu, pulang dengan rasa penasaran yang mengganjal.

Di kost-kost-an, dengan penuh rasa penasaran ingin tahu, saya pun mengutak-atik rumus “cepat” yang telah ia gunakan tersebut. Setelah beberapa waktu lamanya, akhirnya, terpecahkan juga rahasia rumus “cepat” yang dipakai teman saya tersebut. Saya berhasil menelusuri asal-muasal rumus “cepat” tersebut, berhasil menguak rahasianya. (Duh rasanya begitu senang sekali, tak bisa saya ekspresikan dengan kata-kata).

Hasil penelusuran saya tersebut, setelah saya rapikan, seperti berikut ini.

(a + b)³ = (a + b)²(a + b)

= (a² + 2ab + b²)( a + b)

= a³ + a²b + 2a²b + 2ab² + b²a + b³

= a³ + b³ + 3a²b + 3ab²

= a³ + b³ + 3ab (a + b)

Jadi, (a + b)³ = a³ + b³ + 3ab (a + b).

Sehingga, a³ + b³ = (a + b)³ – 3ab (a + b). Rumus “cepat” (1) dapat saya buktikan kebenarannya. Kemudian, dengan cara serupa, saya pun berhasil menelusuri asal-muasal rumus “cepat” (2).

Walaupun apa yang telah saya lakukan tersebut sederhana, tapi bagi ukuran saya waktu itu adalah sesuatu yang menggembirakan hati, menyenangkan pikiran, dan memuaskan dahaga keingin-tahuan saya.

Sejak saat itu, bila ada rumus-rumus “cepat” yang saya temui di buku-buku bimbingan tes, saya pun terpacu untuk menelusuri asal-muasalnya. Dengan cara seperti itu, saya seringkali berhasil memecahkan rahasia rumus-rumus “cepat” yang selama ini beredar luas di kalangan siswa yang mengikuti bimbingan test.

Baiklah, segitu dulu saja ceritanya ya…, lain kali insya Allah saya akan membahas baik-buruknya penggunaan rumus “cepat” (Ada satu cerita yang sangat menggelikan tentang hal ini. Mau tahu? Silakan tunggu di postingan mendatang…). Sampai di sini dulu ya…, mudah-mudahan bermanfaat.

Sebagai bahan latihan untuk Anda, cobalah telusuri asal-muasal rumus-rumus “cepat” berikut ini.

1. Persamaan garis yang melalui titik (0, a) dan (b, 0) adalah ax + by = ab.
2. Perhatikan gambar berikut. Panjang PQ dapat ditentukan dengan mudah, yaitu:
   PQ = (AP. DC + DP. AB)/(AD)

Catatan:

*UMPTN: Ujian Masuk Perguruan Tinggi Negeri (Saat ini namanya SPMB)

**EBTANAS: Evaluasi Belajar Tahap Akhir Nasional (Saat ini namanya UAN)

========================================================

Update: Artikel ini bisa juga dibaca di sini.

========================================================

Update:

Makin hari, makin banyak orang-orang yang secara tidak sopan menerbitkan ulang artikel saya ini. Mereka mempublikasi ulang tanpa menuliskan nama penulis dan sumbernya dan tidak memberi link sama sekali. Oleh karena itu, bila Anda menerbitkan ulang artikel ini, tolong minta ijin terlebih dulu ke saya. Bila Anda tidak minta ijin, saya tidak rela, saya tidak ikhlas, saya tidak mengijinkannya. Atas perhatiannya saya ucapkan terimakasih!!!!

Rabu, 03 April 2013

Baru-baru saja aku menonton tayangan televisi di sebuah stasiun televisi swasta. Tayangan itu cukup menarik karena membahas trik cepat mengerjakan soal-soal ujian matematika tentang materi perbandingan. Namun saat pembahasan dengan trik cepat aku malah tertawa keras. Saking kerasnya membuat salah seorang teman kos ku terkejut dan sehingga dia tertarik ikut menonton. Dan tahukah kamu apa yang terjadi? Dia juga ikut tertawa. Hua...ha...ha...ha.... Mau tau ceritanya?

Begini ceritanya. Pada jaman dahulu kala ........... (alah.....jadi ngawur. Sorry)

Ada soal seperti ini (kira-kira aja ya kata-katanya, lupa. Tapi konsepnya tetap diusahakan sama) 

2 orang pekerja mampu menyelesaikan suatu proyek selama 12 hari. Jika pekerjanya ditambah 6 orang, berapa lama proyek itu selesai?

Penyelesaiannya dengan cara biasa seperti ini.

Diketahui :

n1 = 2 orang

t1 = 12 hari 

n2 = 2 + 6 = 8 orang

Tanya : n2 (waktu yang diperlukan setelah ditambah pekerjanya)?

Jawab. Karena semakin banyak pekerja maka waktu yang dihabiskan makin sedikit maka hal ini merupakan perbandingan terbalik. (ciri-cirinya perbandingan terbalik adalah jika variabel x semakin naik tetapi variabel y semakin turun).

Kalau begitu maka perkalian pasangan masing-masing komponen akan menghasilkan konstanta yang sama. Artinya: 

 

Jadi, perlu waktu sebanyak 3 hari.

Nah, setelah itu muncul ungkapan: 

Bukan SAYA (maaf nama tayangan dirahasiakan) kalau tidak ada trik cepatnya. Begini caranya:

Karena ini perbandingan terbalik, maka 

Hebat bukan? Cuma satu baris (dengan bangganya dia tertawa).

Melihat trik cepat ini, kontan saja saya tertawa. Ini kan cara yang sama seperti cara sebelumnya, hanya beberapa langkah dihilangkan. Coba perhatikan langkah kedua pada cara sebelumnya. Kalau 8 kita pindahkan pakai kali silang*, maka 8 kan berada di bawah. Jadinya sama dengan cara di atas. Cara pertama terlihat panjang karena urutan pekerjaan diperlihatkan. Kemudian teknik pindah silang baru dijalankan pada langkah ke empat.

Hua...ha...ha.... lucu kan (mudah-mudahan anda juga merasa lucu).

Kalau anda merasa lucu, maka seharusnya anda tertawa juga pada hampir semua trik cepat yang ada sekarang ini. Hampir semuanya memiliki karakteristik seperti di atas. Trik cepat biasanya merupakan cara yang panjang tetapi beberapa baris dihilangkan. Lalu cara cepat itu ditulis dengan rumus tersendiri yang sepertinya terpisah dari rumus sebenarnya (coba aja kita mau tekun, maka kita dapat menemukan semua cara atau trik cepat melalui penurunan rumus sebenarnya).

Terlepas dari itu semua, jika kita perhatikan dengan seksama baik menggunakan rumus sebenarnya maupun trik cepat, maka keduanya merupakan suatu algoritma. Dikatakan algoritma karena adanya urutan langkah-langkah tertentu dalam mengerjakan. Nah, kalau lupa pada langkahnya, matilah kita. Pasti kita tidak mampu mengerjakannya. Apalagi untuk trik cepat karena lain soal lain pula trik cepatnya. Artinya, jauh lebih banyak menghapal trik cepat dibandingkan hanya menghapal rumusnya. Sekali lagi, kalau lupa cara cepatnya atau karakteristik soalnya, Matilah kita. (weleh...weleh.... matinya dua kali. Mungkin karena ini ya plesetan kata matematika adalah mati-matian)

Kalau seandainya pembelajaran matematika tidak menitikberatkan pada rumus dan urutan-urutan langkah penggunaan melainkan pada berpikir dan bernalar kreatif siswa, maka hal ini tidak perlu terjadi. Siswa tidak perlu banyak menghapal karena mampu berpikir dan bernalar sendiri untuk menyelesaikan soal. Artinya siswa dibebaskan untuk menentukan penyelesaian berdasarkan pemikiran dan penalarannya sendiri. Coba perhatikan contoh soal di atas, kita akan menyelesaikannya dengan logika.

”Kalau 2 orang selesainya 12 hari, maka kalau pekerja menjadi 4 orang selesainya menjadi 6 hari. Ya kan.... nah kalau 4 orang selesainya 6 hari maka tentunya kalau pekerjanya menjadi 8 orang, berarti selesainya menjadi 3 hari”. Selesai bukan. Pakai nalar aja bisa kok.

Coba juga persoalan berikut.

Andi memandang dari jendela sebuah taman dekat rumahnya. Dia melihat bahwa masing-masing orang di taman membawa seekor anjing piaraannya. Setelah itu dia menghitung banyaknya semua kaki di taman itu dan ternyata ada 54 buah. Berapa banyaknya anjing peliharaan yang ada di taman?

Hayo, bagaimana mengerjakannya. Pasti di antara anda sudah keluar tuh lambang-lambang x dan y. Ya kan? Lalu karena manusia punya dua kaki dan anjing punya empat kaki pasti ada yang memikirkan 2x + 4y = 54. benar kan? Nah, sekarang bagaimana persamaan lainnya????.............

Kalau anda memikirkan cara di atas, maka kalau boleh saya katakan di kepala anda sudah tertanam algoritma yang kuat. Jika anda menemukan persamaan satunya maka anda dapat menyelesaikannya dengan teknik substitusi atau teknik lainnya. Tapi kalau tidak, apa yang terjadi?

Sebenarnya kalau kita mau berpikir dan bernalar kreatif, maka kita dapat menggunakan logika saja. Misalnya seperti ini......

Manusia punya 2 kaki

Seekor anjing punya 4 kaki

Satu pasang (manusia dan anjing peliharaan) totalnya 6 kaki. Karena terdapat 54 kaki berarti ada 9 pasang. 

Jadi ada 9 ekor anjing peliharaan.

Selesai. tanpa ada rumus-rumus yang bikin ribet.

Jika kita mau menggunakan logika yang diwujudkandalam berpikir dan bernalar maka hampir semua permasalahan dapat kita selesaikan. Terutama permasalahan yang berkaitan dengan kehidupan sehari-hari. Bukan kah untuk menyelesaikan masalah yang dihadapi kita menyelesaikannya dengan logika dan berpikir, bukannya dengan rumus-rumus yang njelimet?

Bebaskan para siswa berpikir dan bernalar. Biarkan kedua komponen itu berkembang dengan baik dalam diri siswa. Karena keduanya diperlukan oleh siswa untuk menghadapi kehidupan.

*) teknik perhitungan memindahkan bilangan dalam perhitungan baik dari ruas kiri ke kanan atau sebaliknya adalah teknik yang tidak sesuai konsep matematika. Seperti perkalian silang sehingga bagi jadi kali. Atau pada penjumlahan, seperti yang tadinya positif jadi negatif.